√99以上 度数分布表 平均値 求め方 711018-度数分布表 平均値 求め方

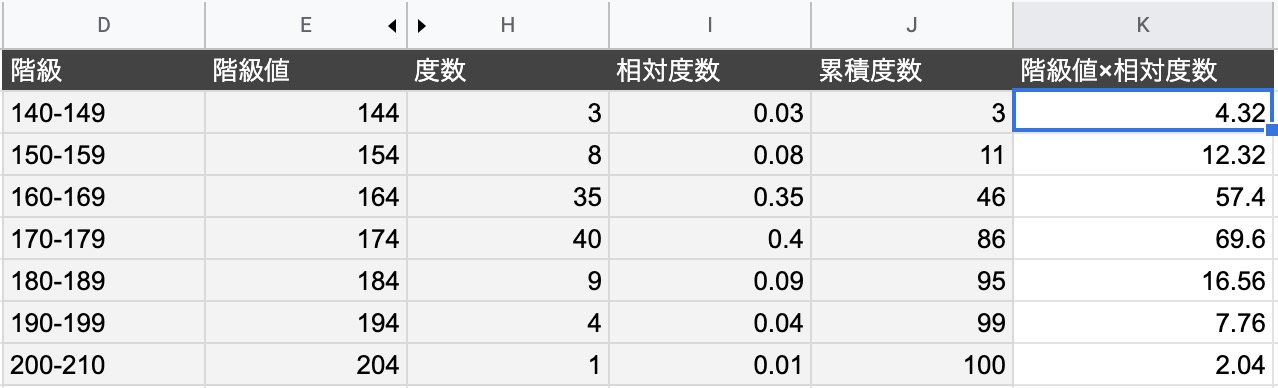
度数分布表から平均値を求める 中卒でも分かる統計学入門 プログラマーになった 中卒 男のブログ

 というか、もし「通勤時間9分」という風に、 確実に時間を言い切るものでしたら、平均（総通勤時間÷人数）で 求めていると思いますが。 もう一度、度数分布表を用いた平均値の求め方の概念を 教科書で確認しましょう。 質問者：ponyottominimum表32 サイコロを100回投げたときに出た目の度数分布表 サイコロの目 度数 相対度数 累積度数 累積相対度数 1 0 0 2 18 018 38 038 3 10 010 48 048 4 14 014 62 062 5 21 021 0 6 17 017 100 100 合計 100 100 注〆度数は各目が出る確率が等しいという条件で

度数分布表 平均値 求め方

度数分布表 平均値 求め方- 度数分布表から平均を求めるとき ってどうすればいいんだろ？？ テストや宿題ででてくるのに、教科書にのってない。。 こいつは困ったね。 そこで今日は、 度数分布表からの平均値の求め方 を5ステップで解説してみたよ。．度数分布表 (量的)変数(例：世帯人員数)がとる値の範囲をグループ分けしたそれぞれの区間を階級 という． 階級に含まれる観測値の個数をその階級の度数(頻度)といい，階級ごとに度数を整理し たものを度数分布，その表を度数分布表という．

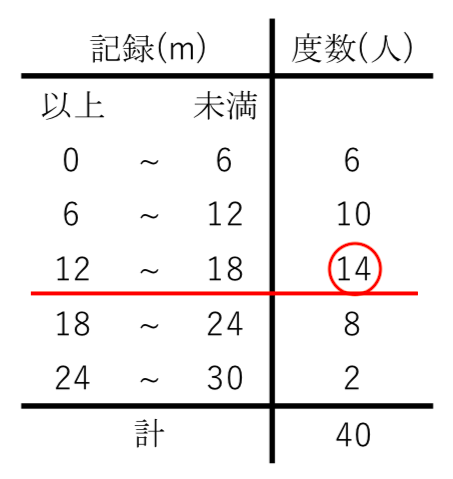
中央値の求め方と最頻値の求め方を誰か教えて下さい よろしくお願いします Clearnote

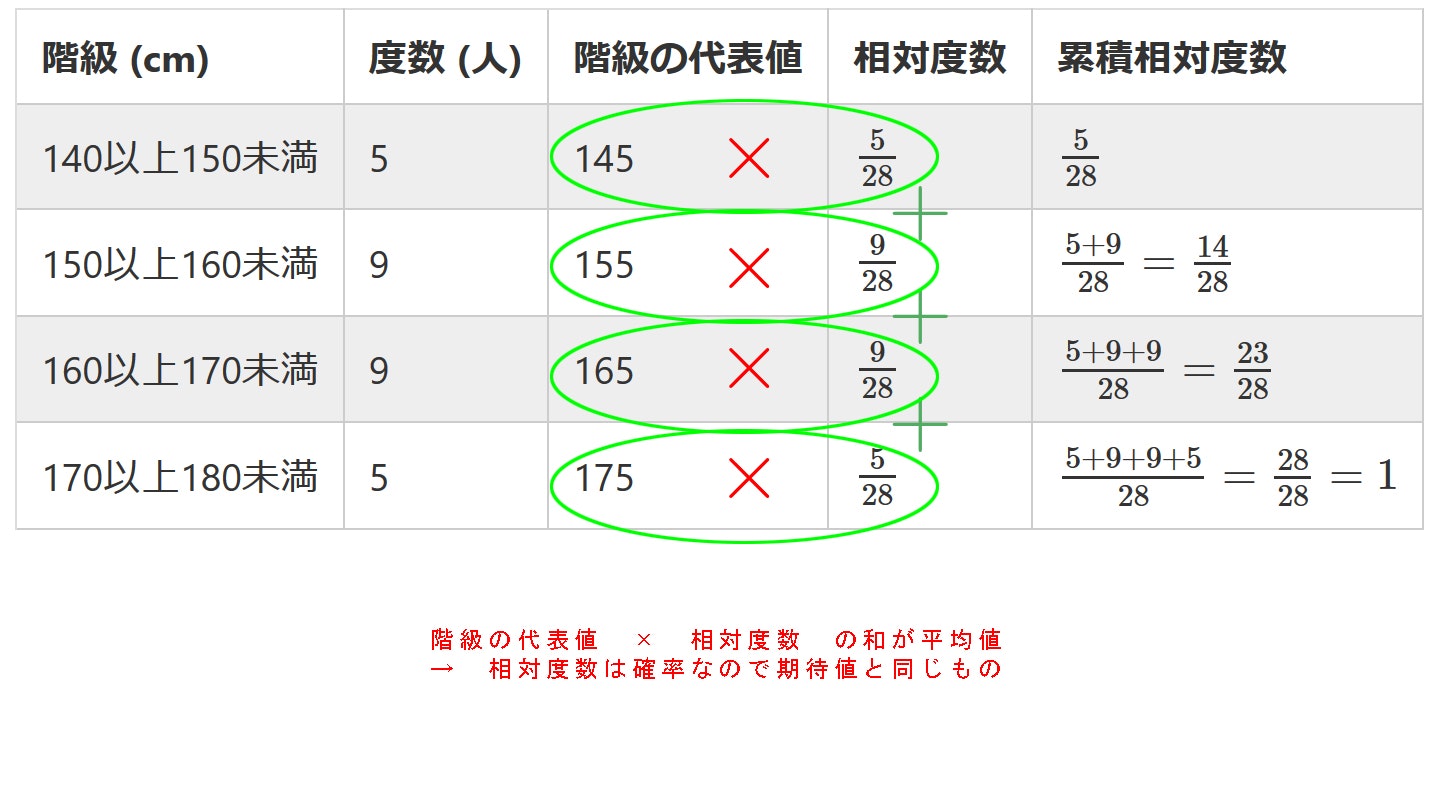
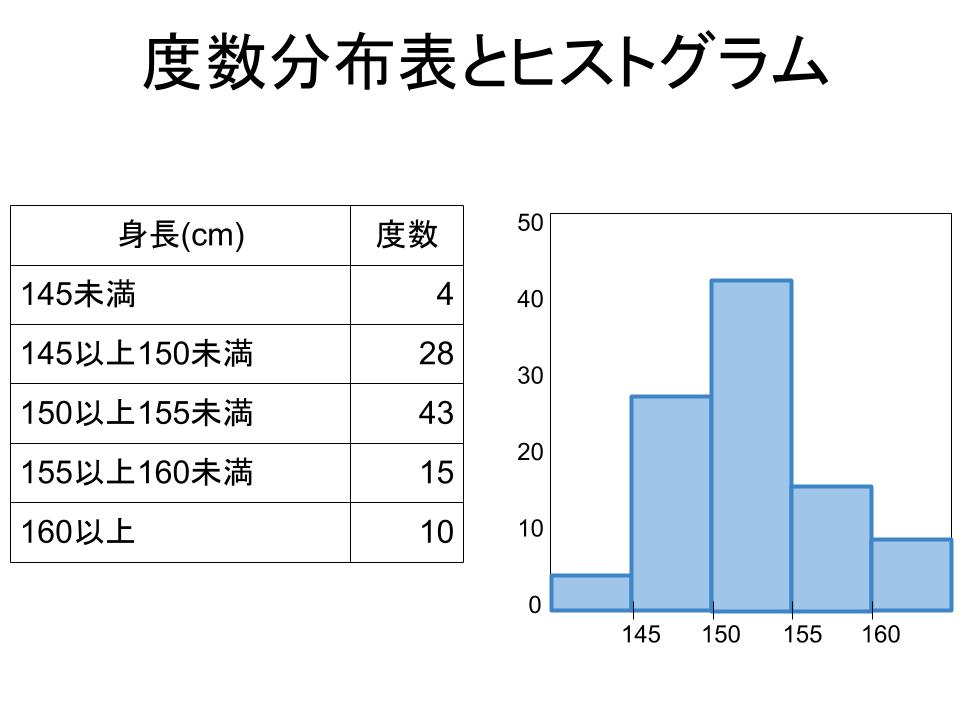
 度数分布表から平均値を計算する方法 度数分布表から平均値を計算する方法についてもご紹介しておきます。 「平均値」というと「 全てのデータを足して、それをデータ数で割る 」のが普通に思いつく方法ですよね。 しかし、平均値の求め方はこの方法 ヒストグラムとは？ 作り方（書き方）や階級・データ区間の決め方 21年5月日 この記事では、「ヒストグラム」についてわかりやすく解説していきます。 ヒストグラムの作り方や、階級・データ区間の決め方、代表値（平均値・中央値・最頻値）のこの記事では「相対度数とは？ 度数分布表から求め方や意味をわかりやすく！ パーセント表示する？ 」ということを解説します。 相対度数はなんとなくわかるようで、わかりにくい。 。 ということで、この記事を見れば以下のことがわかるように

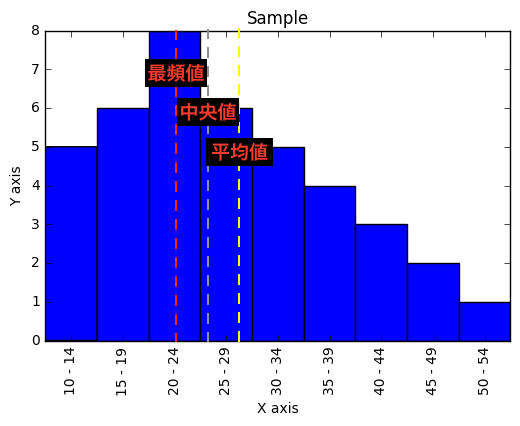
 期待値というのは「確率変数の平均」のことです． 言葉だけではわかりにくいと思うので，丁寧に解説していきます． 例えば，以下のような確率変数Xに対する度数分布表が与えられていたとします． 測定値 度数 相対度数 度数分布表について詳しく 度数分布表から平均値を求める中卒でも分かる統計学入門 19年6月26日 中卒でも分かる統計学入門 数学, 統計学 suckamon 前回、統計学の基礎として縮約と呼ばれる手法のうち、度数分布表とヒストグラムによる分析方法を紹介した。 中卒でも 最頻値（モード）の求め方がわかる2ステップ 最頻値は2ステップでだせちゃうよ。 度数が多い階級をみつける 階級値を計算する 最頻値を求める例として、 砲丸投げに挑戦するアスリートに注目しよう。 AさんとBさんだ。 市内体育祭の出場権をかけて

度数分布表 平均値 求め方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	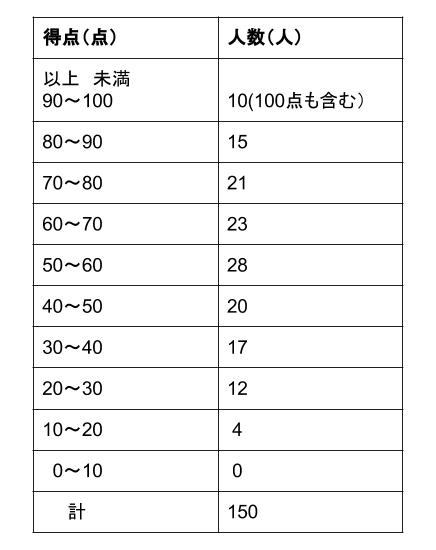度数分布表の平均 資料の整理 中学１年 数学の楽園	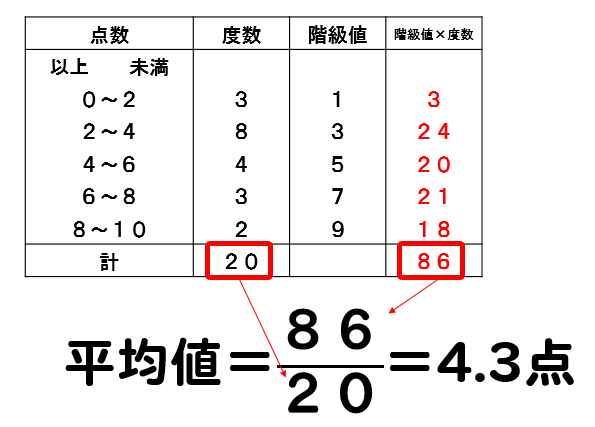度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園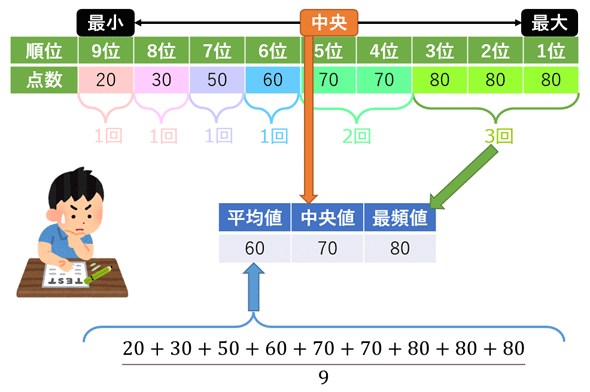
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園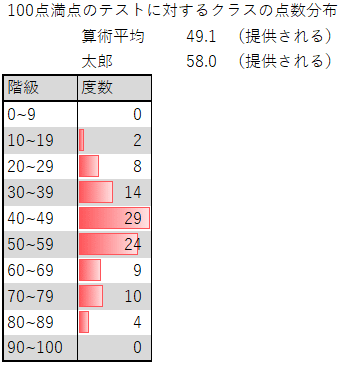
度数分布表の平均 資料の整理 中学１年 数学の楽園	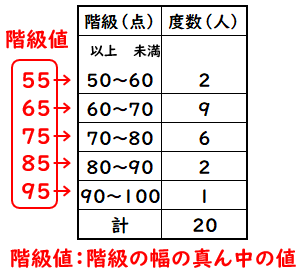度数分布表の平均 資料の整理 中学１年 数学の楽園	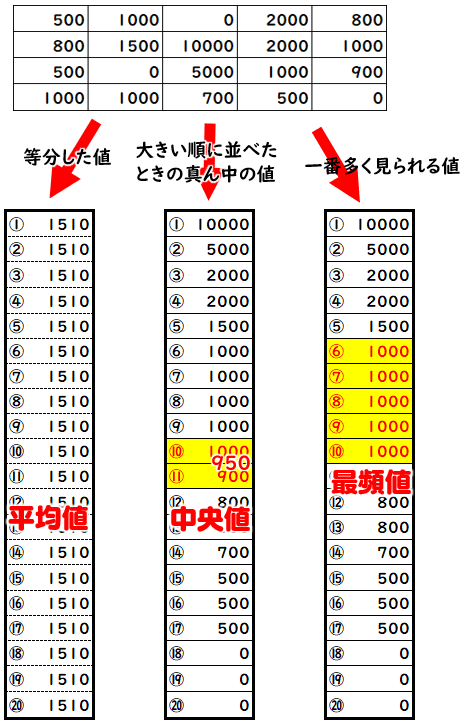度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園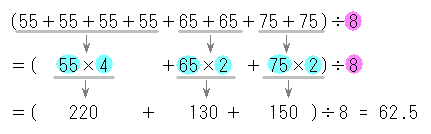
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	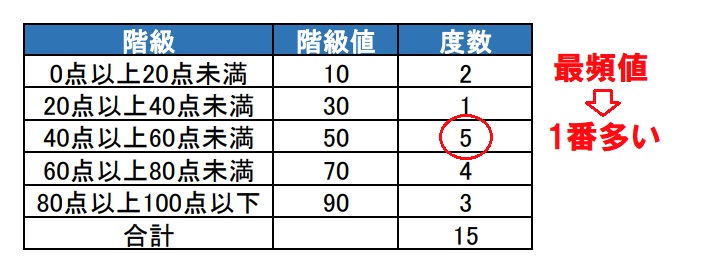度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	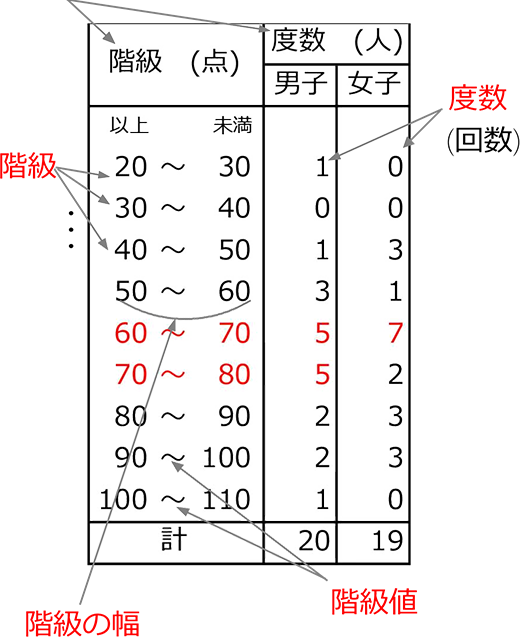度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	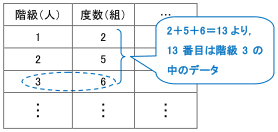度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	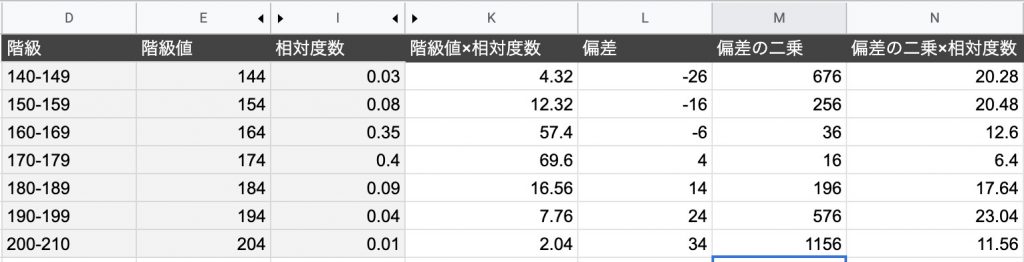度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	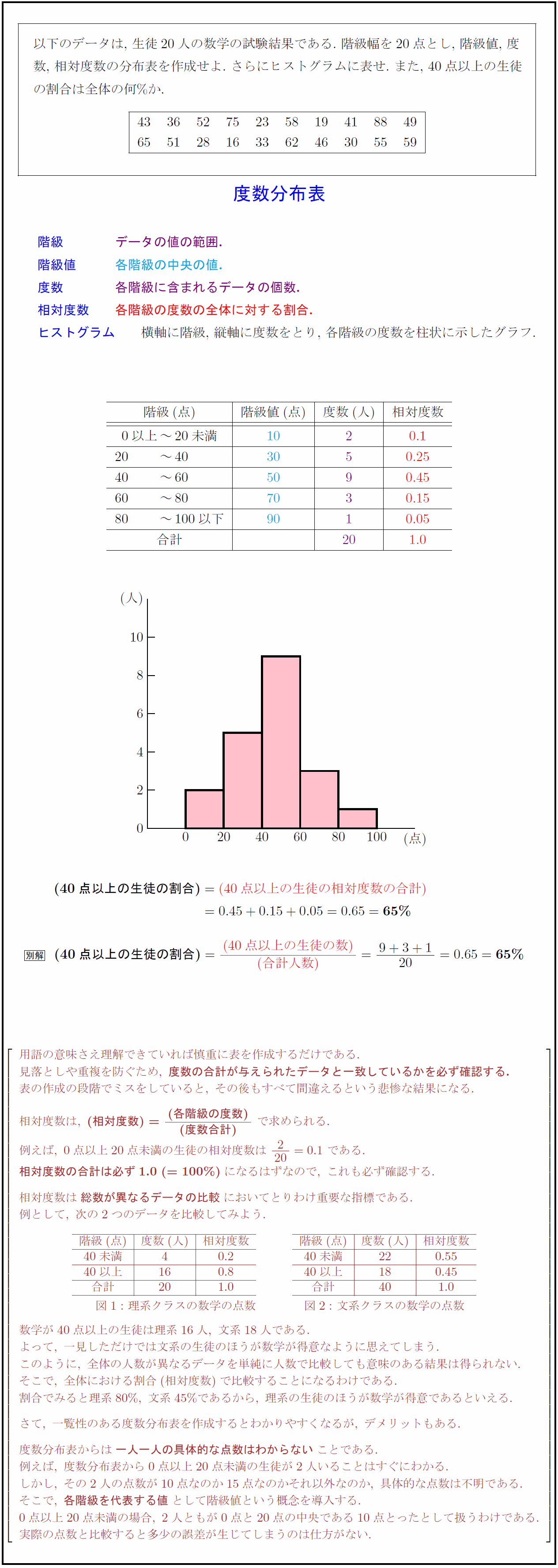度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	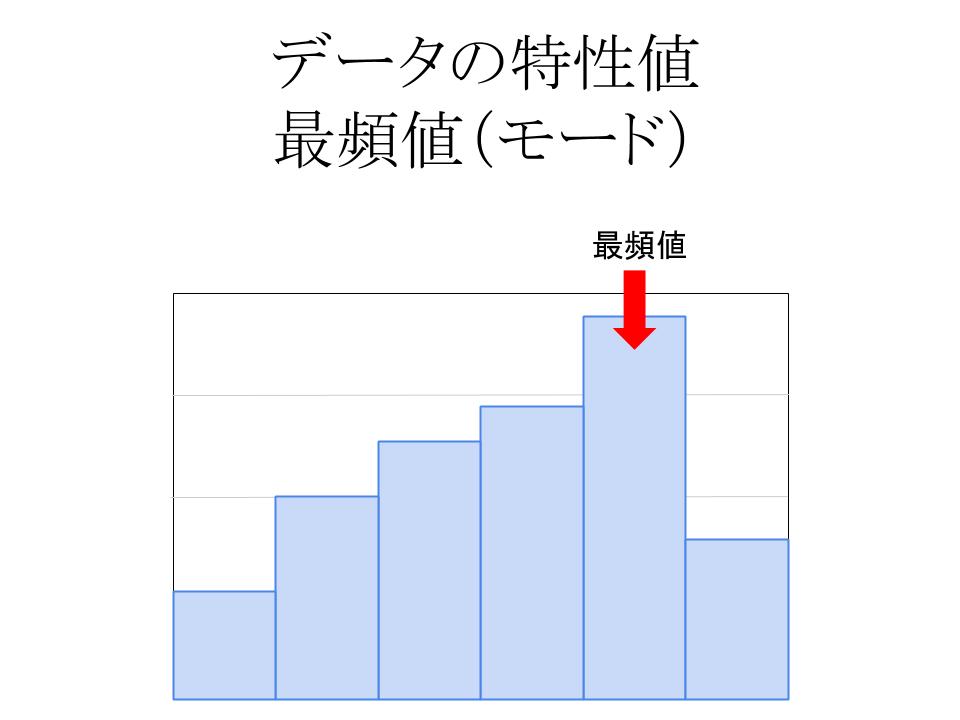度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	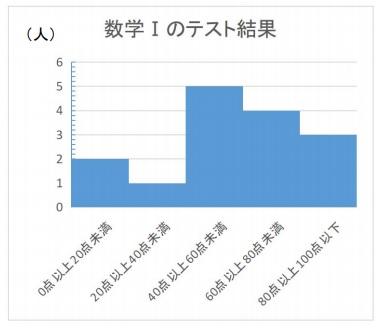度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	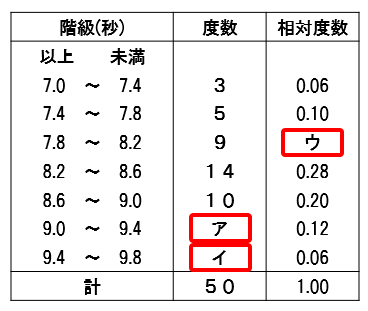度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	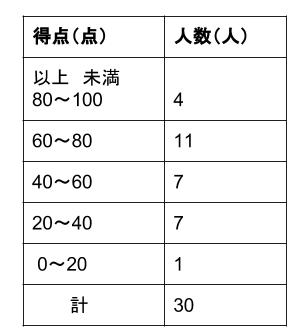度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	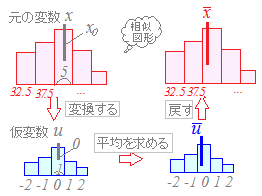度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	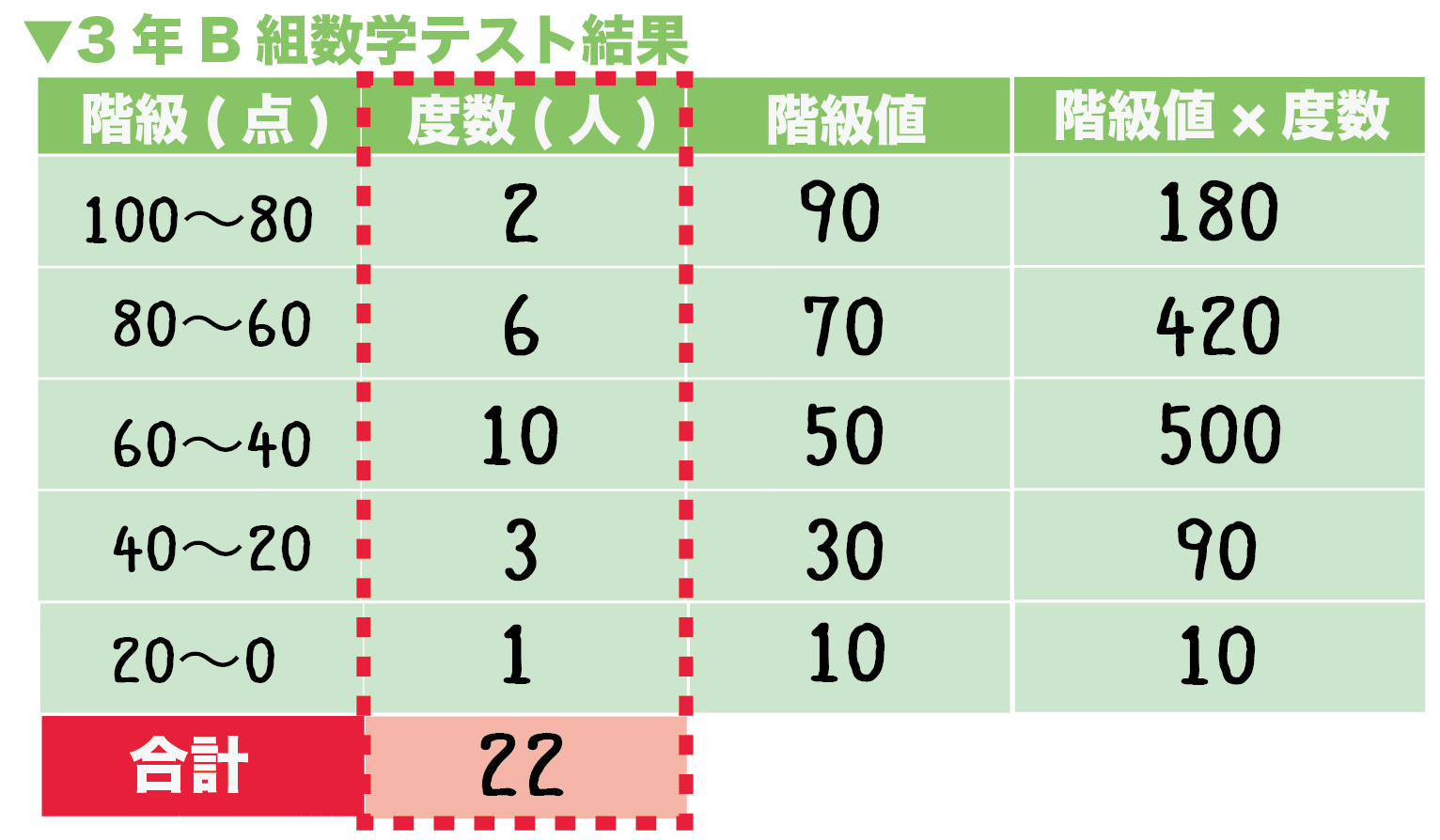度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園
度数分布表の平均 資料の整理 中学１年 数学の楽園	度数分布表の平均 資料の整理 中学１年 数学の楽園

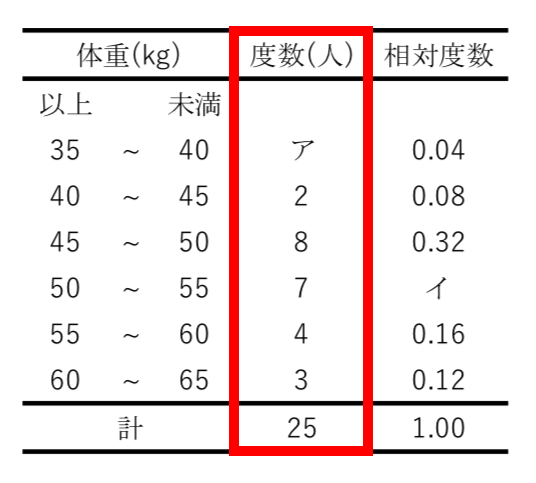
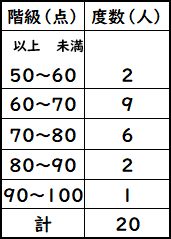
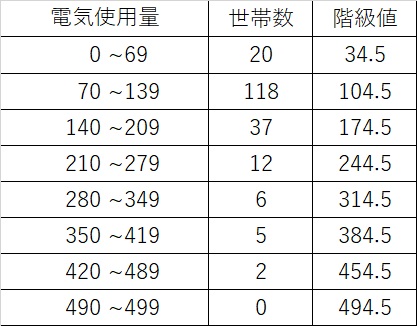
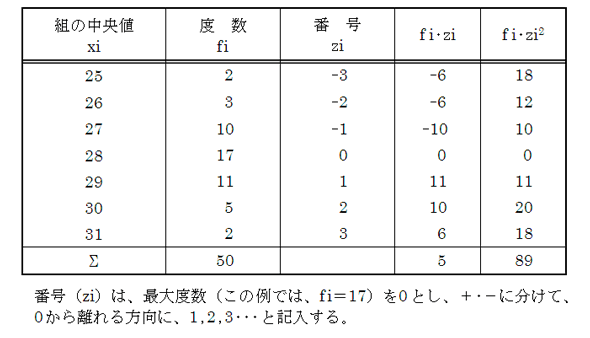
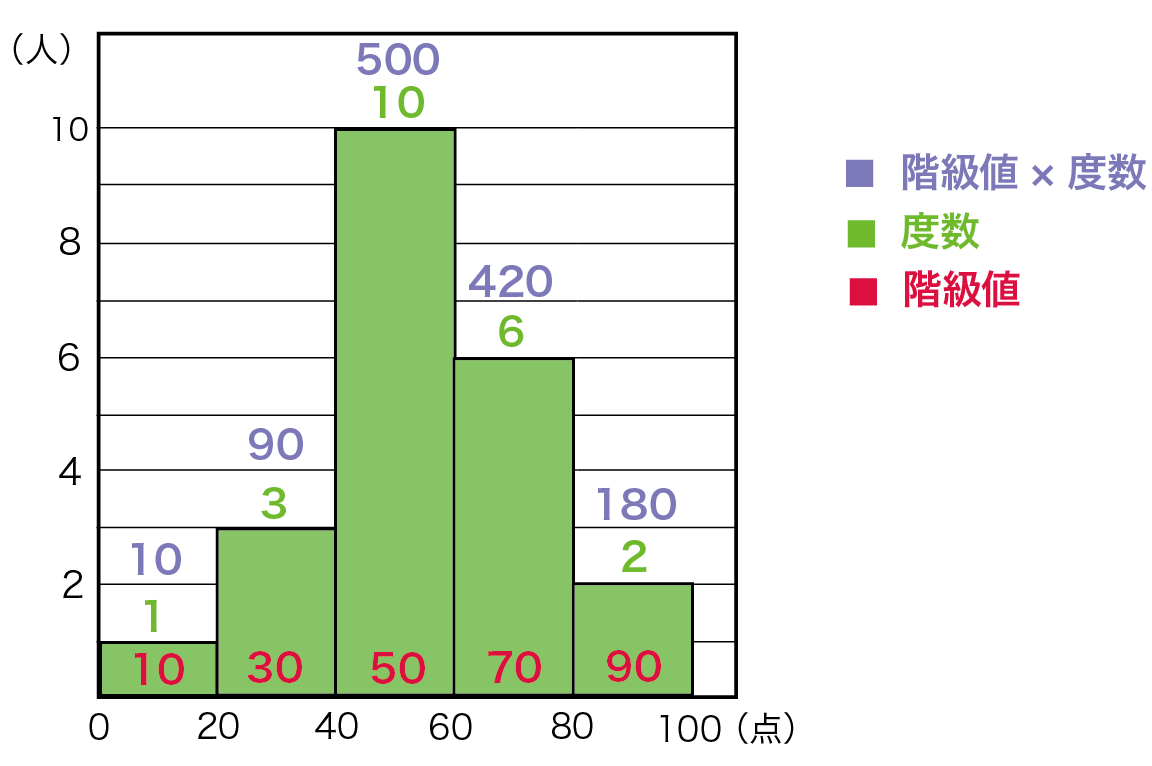
度数分布表の中央付近で，仮変数 0 にすると大きい方も小さい方も ±2 のように小さな整数値になって，計算が楽になるからです．先頭を 0 から始めて（仮平均を他の値に設定しても，例えば325としても）も正しく求めることはできますが，階級値の仮変数2代表値 平均値 ・度数分布表から求める方法 平均値＝ ｛（階級値）×（度数）｝の合計 度数の合計 階級値 階級の中央の値。35～40 kg の階級値は 37 5 kg。 ・仮の平均（平均に近いと考えられる値）を利用 する方法 はじめに，仮の平均を決めて，

Incoming Term: 度数分布表 平均値 求め方,